Υπολογισμός του εμβαδού στο ελλειψοειδές στερεό. Ημιάξονες ελλειψοειδούς. Τι γεωμετρικό σχήμα είναι το ελλειψοειδές; | Surface Area of an Ellipsoid
Υπολογισμός εμβαδού συνολικής επιφάνειας ελλειψοειδούς online
Surface Area of an Ellipsoid online calculator
Ελλειψοειδές – Ellipsoid | Υπολογισμός γεωμετρικών στερεών
Ως ελλειψοειδή χαρακτηρίζονται τα στερεά πού προκύπτουν από περιστροφή της έλλειψης και είναι δηλαδή το τρισδιάστατο αντίστοιχο της έλλειψης. Είναι δηλαδή στερεό εκ περιστροφής.
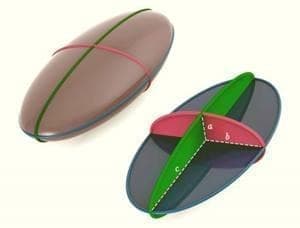
Μία επιφάνεια κλειστή και συμμετρική ως προς τρία τρισορθογώνια επίπεδα, που θεωρούνται και επίπεδα συντεταγμένων.
Εκτός από τα τρία αυτά επίπεδα συμμετρίας, έχει και τρεις άξονες συμμετρίας (τις τομές των τριών επιπέδων ανά δύο) και ένα κέντρο συμμετρίας (την τομή των τριών επιπέδων).
Μία ειδική περίπτωση του ε. είναι το ε. εκ περιστροφής (η επιφάνεια δηλαδή που προκύπτει όταν μία έλλειψη στραφεί γύρω από το μεγάλο ή το μικρό της άξονα).
Η τριάδα των αξόνων συμμετρίας του ε. είναι μοναδική, όταν το ε. δεν είναι εκ περιστροφής.
Ελλειψοειδές εμβαδόν επιφάνειας – μαθηματικός τύπος
Surface Area of an Ellipsoid Calculator – math formula
Το εμβαδόν επιφάνειας (κατά προσέγγιση) του ελλειψοειδούς δίδεται από τον κάτωθι μαθηματικό τύπο :
$$ S= 4 · π ((a^p · b^p + a^p · c^p + b^p · c^p ) /3)^(1/p) $$όπου S το εμβαδόν της επιφάνειας, επίσης a, b, c, το μήκος των ημι-αξόνων και p=1,6075 ένας συντελεστής του Knud Thomsen που με τον ανωτέρω τύπο δίνει κατά προσέγγιση το εμβαδόν της συνολικής επιφάνειας του ελλειψοειδούς
Ελλειψοειδές – Ellipsoid
![]() Στη Γεωδαισία, Ελλειψοειδές αναφοράς είναι μια μαθηματικά προσδιορισμένη επιφάνεια που προσεγγίζει το Γεωειδές.
Στη Γεωδαισία, Ελλειψοειδές αναφοράς είναι μια μαθηματικά προσδιορισμένη επιφάνεια που προσεγγίζει το Γεωειδές.
Λόγω της σχετικής τους απλότητας, τα Ελλειψοειδή αναφοράς χρησιμοποιούνται ως η προτιμώμενη επιφάνεια πάνω στην οποία γίνονται οι γεωδαιτικοί υπολογισμοί. Οι συντεταγμένες που ορίζονται πάνω σε αυτό, ονομάζονται γεωγραφικές συντεταγμένες.
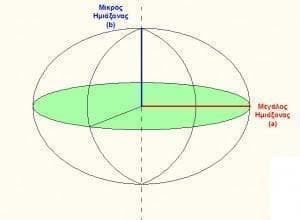 Μπορούμε να καταλάβουμε το σχηματισμό του ελλειψοειδούς αναφοράς, αν φανταστούμε μια έλλειψη, η οποία δημιουργεί την επιφάνειά μας καθώς περιστρέφεται γύρω από το μικρό της ημιάξονα.
Μπορούμε να καταλάβουμε το σχηματισμό του ελλειψοειδούς αναφοράς, αν φανταστούμε μια έλλειψη, η οποία δημιουργεί την επιφάνειά μας καθώς περιστρέφεται γύρω από το μικρό της ημιάξονα.
Πιο απλά μπορούμε να τη φανταστούμε, ως μία ελαστική σφαίρα που πιέζουμε κατά τον άξονα περιστροφής της γης.
Το σύστημα αναφοράς που ορίζεται πάνω στο ελλειψοειδές αναφοράς, είναι το σύστημα των Γεωγραφικών Συντεταγμένων.
Μεσημβρινοί ονομάζονται οι τομές του ελλειψοειδούς με το επίπεδο που σχηματίζει το σημείο που μας ενδιαφέρει και ο άξονας περιστροφής. 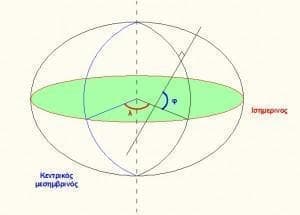 Οι μεσημβρινοί είναι ίσες μεταξύ τους ελλείψεις.
Οι μεσημβρινοί είναι ίσες μεταξύ τους ελλείψεις.
Παράλληλοι είναι οι τομές του ελλειψοειδούς και του κάθετου στον άξονα περιστροφής επιπέδου, που περιέχει το σημείο ενδιαφέροντος.
Οι παράλληλοι είναι κύκλοι των οποίων η ακτίνα μειώνεται όσο πλησιάζουμε στους πόλους.
Ισημερινός ονομάζεται ο μεγαλύτερος παράλληλος, το επίπεδο του οποίου διέρχεται από το κέντρο της γης.
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




