Υπολόγισε το συνολικό εμβαδό του πρίσματος. Εμβαδόν παράπλευρης επιφάνειας συν το εμβαδόν των βάσεων. Ορισμός πρίσμα, πρισματική επιφάνεια, είδη πρίσματος.
Πρίσμα – Υπολογισμός εμβαδόν επιφάνειας πρίσματος online
Area of prism calculator – Online calculation
Πρίσμα – Γεωμετρία – Στερεομετρία – Γεωμετρικά Στερεά
Τα πρίσματα και οι κύλινδροι μπορούν να προκύψουν με εξώθηση (extrusion) των βάσεών τους κατά h, όπου h το ύψος τους.
Το ανάπτυγμα του πρίσματος είναι ένα ορθογώνιο παραλληλόγραμμο, το οποίο αναδιπλώνεται για να αποδώσει όλα τα επιμέρους ορθογώνια, και οι δύο βάσεις συνδεδεμένες σε μία ακμή τους στις απέναντι πλευρές ενός επιμέρους ορθογωνίου. | via
Εμβαδόν παράπλευρης επιφάνειας ορθού πρίσματος – τύπος
Το εµβαδόν της παράπλευρης επιφάνειας ενός πρίσµατος ισούται µε το γινόµενο της περιµέτρου της βάσης του επί το ύψος του πρίσµατος. ∆ηλαδή:
Εμβαδόν συνολικής επιφάνειας ορθού πρίσματος
Το ολικό εµβαδόν ενός πρίσµατος (Εολ) είναι το άθροισµα του εµβαδού της παράπλευρης επιφάνειας Επ και των εµβαδών Εβ των δύο βάσεων. ∆ηλαδή:
Ορισμός και στοιχεία του πρίσματος
- Βάσεις πρίσματος καλούνται οι τομές των δυο παράλληλων επιπέδων με την πρισματική επιφάνεια
- Παράπλευρες έδρες είναι τα τμήματα των εδρών της πρισματικής επιφάνειας, που περιέχονται μεταξύ των βάσεων
- Παράπλευρες ακμές είναι τα τμήματα των ακμών της πρισματικής επιφάνειας, που περιέχονται μεταξύ των βάσεων.
- Έδρες πρίσματος είναι οι βάσεις και οι παράπλευρες έδρες.
- Ακμές πρίσματος είναι οι πλευρές της βάσης και οι παράπλευρες ακμές.
- Κορυφές πρίσματος είναι οι κορυφές των βάσεων.
- Ύψος πρίσματος είναι η απόσταση των βάσεων.
- Διαγώνιος πρίσματος είναι κάθε ευθύγραμμο τμήμα που τα άκρα του δεν είναι κορυφές της ίδιας έδρας.
- Διαγώνιο επίπεδο πρίσματος είναι κάθε επίπεδο που ορίζεται από δυο παράπλευρες ακμές, που δεν ανήκουν στην ίδια παράπλευρη έδρα
Πρισματική επιφάνεια
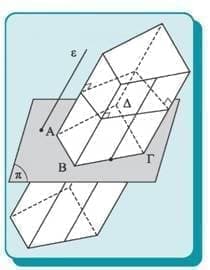
Θεωρούμε σε ένα επίπεδο π μία κλειστή πολυγωνική γραμμή με ν κορυφές και μία ευθεία ε, που τέμνει το π.
Το σύνολο των ευθειών που είναι παράλληλες στην ε και διέρχονται από τα σημεία της πολυγωνικής γραμμής λέγονται γενέτειρες (σχήμα αριστερά) και συνιστούν μία επιφάνεια που λέγεται πρισματική επιφάνεια.
Η πολυγωνική γραμμή λέγεται οδηγός γραμμή. Οι γενέτειρες που διέρχονται από τις κορυφές της πολυγωνικής γραμμής λέγονται ακμές της πρισματικής επιφάνειας.
Το σύνολο των γενετειρών, που τέμνουν μία πλευρά της πολυγωνικής γραμμής, σχηματίζει μία επίπεδη επιφάνεια που λέγεται έδρα της πρισματικής επιφάνειας.
Πρίσμα
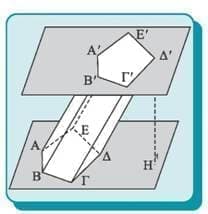
Οι δύο ίσες και παράλληλες τομές λέγονται βάσεις του πρίσματος. Κάθε ευθύγραμμο τμήμα που έχει άκρα στα επίπεδα των βάσεων και είναι κάθετο σε αυτά λέγεται ύψος του πρίσματος.
Τα τμήματα των εδρών της πρισματικής επιφάνειας που περικλείονται μεταξύ των επιπέδων των βάσεων είναι παραλληλόγραμμα και λέγονται παράπλευρες έδρες του πρίσματος.
Τα τμήματα των ακμών της πρισματικής επιφάνειας που περιλαμβάνονται μεταξύ των επιπέδων των βάσεων λέγονται παράπλευρες ακμές του πρίσματος. | via
Ειδικές κατηγορίες πρισμάτων
Ορθό καλείται ένα πρίσμα, όταν οι παράπλευρες ακμές είναι κάθετες στις βάσεις.
Κανονικό καλείται ένα πρίσμα, όταν είναι ορθό και επιπλέον οι βάσεις είναι κανονικά πολύγωνα.
Παραλληλεπίπεδο καλείται ένα πρίσμα, όταν οι βάσεις του είναι παραλληλόγραμμα
Μορφές – είδη Πρίσματος
Η ειδικότερη ονομασία ενός πρίσματος προσδιορίζεται από το πλήθος των πλευρών της βάσης.
Πενταγωνικό πρίσμα, τριγωνικό πρίσμα, εξαγωνικό πρίσμα κλπ. Από την παραλληλία των βάσεων και την παραλληλία των παράπλευρων ακμών στα πρίσματα προκύπτει
Σε κάθε πρίσμα ισχύουν οι προτάσεις:
- οι παράπλευρες έδρες είναι παραλληλόγραμμα,
- οι παράπλευρες ακμές είναι ίσες,
- οι βάσεις είναι ίσες.
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




