Υπολόγισε τις διατάξεις. Υπολογισμός online για το πλήθος των διατάξεων που μπορούν να γίνουν από δεδομένο πλήθος αντικειμένων - δείγματος - στοιχείων.
Υπολόγισε online τον αριθμό των διατάξεων που μπορούν να γίνουν
Statistics – Permutation Calculator
Υπολογισμός online – βρες το πλήθος των διατάξεων που μπορούν να προκύψουν από ένα δεδομένο πλήθος αντικειμένων (με σημαντική την εσωτερική σειρά διάταξης των στοιχείων). Permutation Calculator
Διαφορά μεταξύ συνδυασμών και διατάξεων
Όπως προκύπτει και από τα αναγραφόμενα μας παρακάτω, θα πρέπει εξ αρχής να γίνει ξεκάθαρη στο μυαλό μας, ποια η διαφορά μεταξύ των συνδυασμών και των διατάξεων.
Με απλά λόγια:
Στους «συνδυασμούς» το ζητούμενο είναι ο αριθμός των συνδυασμών και όχι των διατάξεων δηλαδή η εσωτερική σειρά διάταξης ΔΕΝ είναι σημαντική
Παράδειγμα Προβλήματος Συνδυασμών
Οι πιθανές ομάδες δύο ατόμων που μπορούν να σχηματιστούν από 8 υποψηφίους (που δεν μας ενδιαφέρει ποιος από τους δύο είναι 1ος ή 2ος στην διάταξη)
Δείτε στο Ypologismos.gr: Υπολόγισε τον αριθμό συνδυασμών για δεδομένο πλήθος αντικειμένων
Στις «διατάξεις» το ζητούμενο είναι ο αριθμός των διατάξεων και όχι των συνδυασμών δηλαδή η εσωτερική σειρά διάταξης είναι σημαντική
Παράδειγμα Προβλήματος Διατάξεων
Οι πιθανή συνδυασμοί μίας κλήρωσης ΤΖΟΚΕΡ, ΛΟΤΤΟ, Λαϊκό Λαχείο κλπ (που μας ενδιαφέρει ποιος αριθμός είναι στην κάθε διάταξη – σειρά)
Διάταξη – Στατιστική – Μαθηματικά
Μια διάταξη των n στοιχείων συνόλου Ζ {z1,z2…zn} ανά k είναι ένα διατεταγμένο δείγμα (z1,z2…zk) που προκύπτει από την επιλογή k στοιχείων από το σύνολο Z, όπου n και k είναι θετικοί ακέραιοι και k μικρότερο ή ίσο του n.
Απλή διάταξη και διάταξη με επανάληψη
Η επιλογή των στοιχείων στην απλή διάταξη γίνεται χωρίς επανάθεση των ήδη επιλεγμένων (επανατοποθέτησή τους στο σύνολο Ζ), σε αντίθεση με την διάταξη με επανάληψη όπου κάθε φορά μπορούμε να επιλέξουμε ένα στοιχείο που ήδη έχει επιλεγεί.
Με πιο απλά λόγια, αν Ζ είναι ένα σύνολο με n στοιχεία, τότε λέμε διάταξη των n στοιχείων του Ζ ανά k, καθέναν από τους διαφορετικούς τρόπους με τους οποίους μπορούμε να πάρουμε k διαφορετικά στοιχεία του Ζ και να τα βάλουμε σε μια σειρά.
Δύο διατάξεις ταυτίζονται όταν έχουν τα ίδια στοιχεία και με την ίδια σειρά.
Μαθηματικός τύπος υπολογισμού διατάξεων
Το πλήθος των διατάξεων των n στοιχείων ανά k είναι
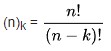
Αν έχουμε n=k, τότε προφανώς οι διατάξεις των n ανά n είναι οι μεταθέσεις όλων των στοιχείων (=n) του συνόλου δηλαδή n!
Για να ισχύει και στην περίπτωση αυτή ο τύπος n!/(n-k)! ορίζουμε ότι 0!=1
Η έκφραση n! διαβάζεται νι παραγοντικό και είναι το γινόμενο όλων των θετικών ακεραίων μικρότερων ή ίσων με ν. via
Συνάρτηση PERMUT στο Excel
Διάταξη είναι κάθε σύνολο ή υποσύνολο αντικειμένων ή γεγονότων, όπου η εσωτερική σειρά των αντικειμένων ή γεγονότων είναι σημαντική.
Οι διατάξεις διαφέρουν από τους συνδυασμούς, για τους οποίους η εσωτερική σειρά των αντικειμένων ή γεγονότων δεν είναι σημαντική.
Χρησιμοποιήστε αυτήν τη συνάρτηση για υπολογισμούς πιθανοτήτων τύπου κλήρωσης.
PERMUT(αριθμός; επιλεγμένος_αριθμός)
Η σύνταξη της συνάρτησης PERMUT περιλαμβάνει τα παρακάτω ορίσματα:
Αριθμός Υποχρεωτικό. Ένας ακέραιος που αντιπροσωπεύει τον συνολικό αριθμό αντικειμένων.
Επιλεγμένος_αριθμός Υποχρεωτικό. Ένας ακέραιος που αντιπροσωπεύει τον αριθμό των αντικειμένων κάθε διάταξης.
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




